安徽省考考试网为您发布安徽省考专业分类目录2023,同步安徽人事考试网信息:2023省考考试时间。更多关于安徽省考,安徽省考公告,安徽公务员考试,安徽省考考试时间的信息内容,请关注安徽省考考试网以及安徽华图,值得信赖!
安徽省考专业分类目录2023
安徽人事考试网:2023安徽公务员考试公告尚未发布,预计在2023年2月-3月发布,具体发布时间以官方网站通知为准!待公告发布后,华图教育将同步安徽人事考试网更新2023年安徽公务员考试公告、职位表等相关信息,请广大考生多多关注!
点击预约》》》2023年安徽省公务员考试公告预约入口https://ah.huatu.com/zt/ahskggyy/
点击查看》》》2023安徽公务员考试公告https://ah.huatu.com/zt/ahskgg/
点击查看》》》安徽省公务员考试历年分数线https://ah.huatu.com/zt/skzwb/
点击检索》》》2023安徽公务员考试职位查询https://ah.huatu.com/zt/zwb/(当前可查询2022年)
点击查询》》》安徽公务员考试专业分类目录https://ah.huatu.com/zt/ahskzy/(当前可查询2022年)
2023安徽省考行测备考:常识热点之小仙翁
提到我国的本土教派道家学派的创始人,大家都会立马想到老子,提倡“无为而治”“道法自然”“祸兮福之所倚,福兮祸之所伏”“上善若水”等。随着历史长河滚滚向前,道家思想也在发扬光大。在东晋,有一个道教理论家、著名炼丹家和医药学家,世称小仙翁。他就是葛洪。
葛洪,字稚川,自号抱朴子。他的人生也是坎坷,出生于江南士族,祖上也是在吴国担任要职。他的父亲在吴国入仕,后吴国灭亡,就到晋国做官,可惜好景不长,逝世于葛洪十三岁时。家道中落,葛洪在饥寒交迫中砍柴、种庄稼。卖了柴换取了笔墨纸砚。虽然人生艰辛,但他并没有放弃,认字、读书,不耻下问。后拜祖父的徒弟郑隐为师,学习炼丹秘术,得到了郑隐的器重。
他的作品也不少,《抱朴子》是最知名的。不仅继承和发展了东汉以来的炼丹法术,也为后来道教炼丹术的发展产生了很大的影响。在这个过程中,就涉及到我们古代四大发明之一——火药的知识点。至于火药是谁发明的,有争议,所以不必纠结。但火药的发明与炼丹有着密切的联系。我们只需了解早在东晋葛洪的著作中已有记载。《抱朴子·内篇》中“以硝石化为水乃凝之”,这里的硝石就是制造火药最重要的原料。先用硝石将雄黄化为水,再凝固,制取长生药。到了唐朝,药王孙思邈的《丹经》记载,火药用于军事战争。宋朝时火药已经广泛应用,如火炮、火箭、突火枪等。火药是通过战争传入欧洲的,13世纪通过商人先传到阿拉伯国家,后来成吉思汗西征,当时的军队就使用了火药。后来元世祖忽必烈与叙利亚作战过程中,阿拉伯人缴获了火箭。14世纪由阿拉伯传到了欧洲。中国的火药推进了世界历史的进程。
别看他炼丹,在古代求仙的方士其实是医生,所以也到处行医,给病人治病。在这个过程中也促进了中医的发展。中医作为我国三大国粹之一,葛洪的成就也值得钦佩。有医学著作《玉函方》一百卷,已失传。《肘后备急方》共100卷,是古代中医方剂著作,也是中国第一部临床急救手册。内容包括各种急性病症、慢性病急性发作的治疗方法、针灸等,其中有世界上最早治天花的记载。提倡用狂犬脑组织治疗狂犬病,被认为是中国最早的免疫思想。
看完之后大家一定对葛洪有了更深入的了解。所以作为常识,涉及面非常广,需要大家在备考过程中对常规考点有所覆盖,在此基础上更要拓展自己的知识面。怎么拓展?现在的考试要关注时政,从时政中延伸地理、科技、人文历史等考点。对于各位考生来说,可以在刷题过程中通过考题、选项的延伸来拓展知识点。
以上是安徽省考专业分类目录2023的全部内容,更多安徽省考,安徽省考公告,安徽公务员考试资讯请继续查看:安徽人事考试网、安徽省考考试网及安徽华图。
2022年相关考试试题:
35 、某市江滨有一处边长为50米的等边三角形广场。广场里设计有三个大小相等的圆环鹅卵石道路供市民散步,如图所示,各圆相切,各圆与三角形也相切,问沿三个圆环外围石道(不含圆切点之间的弧)散步一圈约为多少米?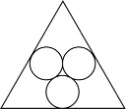
A.95
B.105
C.115
D.125
【答案】:B
【解析】:
解法一:第一步,本题考查几何计算。
第二步,如下图。
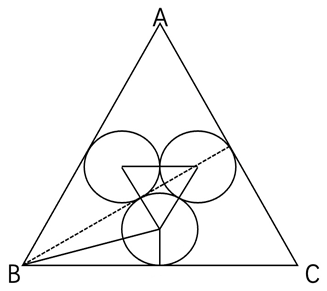
连接三个内切圆的圆心,可知为等边三角形,三个圆之间的弧心角都为60°,可知三个圆之间的弧长各自占三个小圆周长的
 ,剩余部分占三个小圆周长的
,剩余部分占三个小圆周长的 ,根据圆周长公式2πr,则三个圆外弧长石道为2πr×
,根据圆周长公式2πr,则三个圆外弧长石道为2πr× ×3=5πr,求出小圆半径即可。
×3=5πr,求出小圆半径即可。第三步,如下图所示。
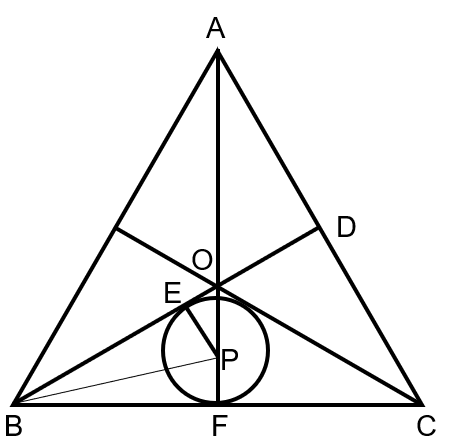
做出等边三角形的三条角平分线,交于一点O。根据等边三角形的性质可知∠EOP=60°;小圆圆心P引垂线交BD于E,由于相切可知三角形EOP是直角三角形,则小圆半径EP=r=
 OE。又因BE=BF=25=
OE。又因BE=BF=25= BO,可知BO=
BO,可知BO= ,则OE=BO-BE=
,则OE=BO-BE= -25,可知r=50-25
-25,可知r=50-25 ≈25×(2-1.732)=6.7。则三个圆外弧长石道为5πr≈105.19。
≈25×(2-1.732)=6.7。则三个圆外弧长石道为5πr≈105.19。因此,选择B选项。
解法二:第一步,本题考查几何计算。
第二步,连接三个内切圆的圆心,可知为等边三角形,三个圆之间的弧心角都为60°,可知三个圆之间的弧长各自占三个小圆周长的
 ,剩余部分占三个小圆周长的
,剩余部分占三个小圆周长的 ,则三个圆外弧长石道为2πr×
,则三个圆外弧长石道为2πr× ×3=5πr,求出小圆半径即可。
×3=5πr,求出小圆半径即可。第三步,如图所示。
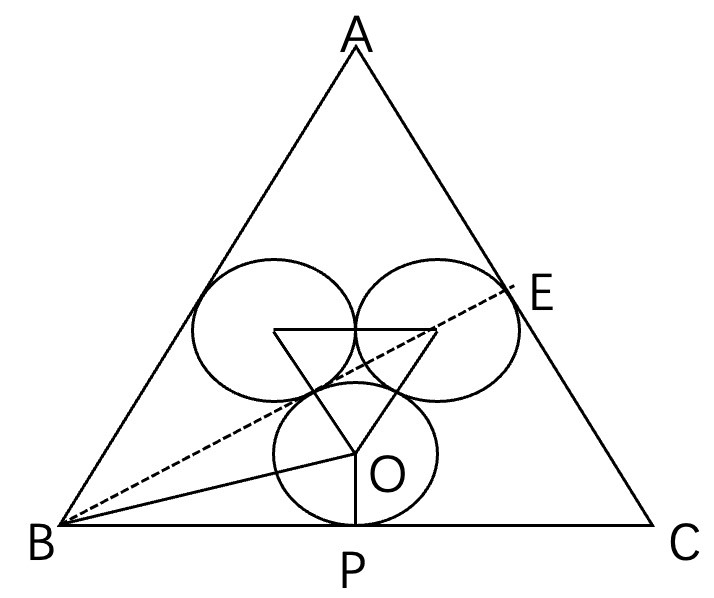
做辅助线BE垂直AC,则∠EBC=30°,小圆圆心O引垂线交BC于P,连接OB,则平分∠EBC,可得,∠OBC=15°,根据tan15°=
 ≈0.268,BP=25,可得OP=6.7,则三个圆外弧长石道为5πr≈5×3.14×6.7=105.19。
≈0.268,BP=25,可得OP=6.7,则三个圆外弧长石道为5πr≈5×3.14×6.7=105.19。因此,选择B选项。
小贴士:如何求解tan15°。tan(α-β)=
 ,则tan15°=tan(60°-45°)=
,则tan15°=tan(60°-45°)= ,tan60°=
,tan60°= ,tan45°=1,可得tan15°=
,tan45°=1,可得tan15°= ≈2-1.732=0.268。
≈2-1.732=0.268。 










