速解一笔画
一笔画问题起源于“七桥问题”——18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸联系起来。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。这个问题的提出,一时间激起大家对此概念的探知欲,很多人开始研究这个命题。而古时的七桥问题逐渐演变成的现在的几何问题——一笔画考点,而这在也是近几年也成为了行测图形推理的热门考点,国联考中的相关真题屡见不鲜,耐人寻味。
一、理解一笔画
顾名思义,一笔画就是一笔不断开、不重复能画出的图形,所有的一笔画图形都是一根线绕成的图形,其中最简单的就是单根线条。而一笔画的作图方式有两种,如下图:
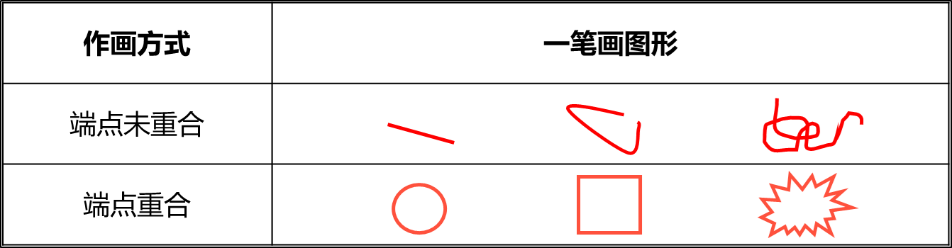
不难发现,一笔画的作图方式比较简单。要么一笔首尾不相连,形成两个端点不重合的图形;要么一笔首尾相连,形成两个端点重合的图形。只要是一笔画都符合上述两种画法中的一种。其实这就为世人后续快速解决一笔画问题埋下了伏笔。
二、判断一笔画
七桥问题提出后,大数学家欧拉解决了此问题,且给出了连通图可以一笔画的充要条件是:图形为一个整体,且奇点的数目不是0个就是2个(连到一点的线条数目如是奇数条,就称为奇点)。几何点按照该点散发线条的数量,可以分为奇点(散发奇数条线)和偶点(散发偶数条线)。如下图所示:
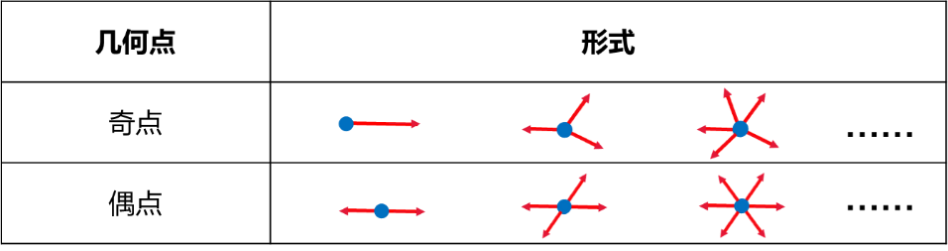
如图,端点引出的线为1条,而1是奇数,故端点是奇点。而“十”的中心点引出的线数为4条,而4为偶数,故该中心点为偶点。由于一笔画两种特殊的作画方式,决定了一笔画的奇点数要么是0、要么是2。利用该规律,就能快速的判断图形是否为一笔画了。
三、掌握一笔画
通过上述内容,相信大家对一笔画都有了更为深刻的理解,即快速判断一笔画的规律为两点:图形为整体,且图形奇点数为0或2。光说不练假把式,下面动手操练起来!
例:.观察图形找出规律,满足问号处规律的图形是?
观察题干图形,不难发现图形间差异较大,相对凌乱,故大概率考察数量及属性考点。逐一代入,快速锁定此题考察一笔画。题干中图形均为一个整体,且奇点数分别为0、0、2、2,故问号处的图形也是一笔画。发现选项ABCD均为一个整体,但奇点数分别为4、6、0、4,故只有C项为一笔画,当选。
图形推理模块的考点相对庞杂,其中不乏由数学几何问题演变出的特殊考点,平时在备考过程中,需要深入了解,切不可知其然而不知所以然,学习容不得半吊子思维,。通过上述的内容,可以更加深入掌握“一笔画”这个特殊考点,为成公上岸保驾护航!










